内角の大きさが150度である正多角形は、何角形でしょうか？

【解答その1】

この図形が何角形なのかは分かりませんが、ある一つの角に注目すると、こんな状態になっています。

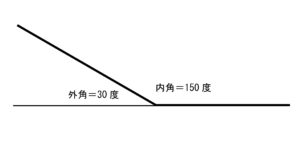
どのような多角形であっても外角の和は360度であることを知っていれば・・

この図形を正ｎ角形だとすると・・

30n＝360
n=12

と解いて、図形が正12角形だったことが分ります。

【解答その2】

あるいは、n角形の内角の和が

180(n-2) により求められることを知っていれば・・

1/ｎ× 180(n-2) ＝150　をnについて解けば良いと考えることができます。

180(n-2)＝150n
30n＝360
n=12

当然ですが、やはり正12角形という答を得られます。

【解答その3】

地道に確認していく方法です。
問の図形が正三角形なら、正方形なら、正五角形なら・・と考えていくやり方です。

正n角形	内角の和	1つの内角の大きさ
3	180	60
4	360	90
5	540	108
6	720	120
7	900	128.57
8	1080	135
9	1260	140
10	1440	144
11	1620	147.27
12	1800	150

面倒ではありますが、こうやって調べても答にたどり着くことはできます。
解答1や解答2のやり方の方が簡単だし、スマートじゃないかと思われる方が多いでしょうし、私もできるならばその方が・・とは思います。

それでも、なかなか解法を着想できないときなどには、解答3のような、『できることをやってみる作戦』は、かなり強力な手法です。時間はかかりますが、「思いつく」という要素はほとんどありません。ですので、難しいな、と思う問題ほど手を動かす習慣をつけましょう。