四角形OABCの各頂点の座標が以下の通りであるとき、
点O(0,0)
点A(-1,5)
点B(2,7)
点C(5,0)
四角形OABCと等しい面積をもつ三角形OADについて、点Dの座標を求めよ。
ただしD(x,0)とする。
【解答】
四角形OABCの姿をグラフ用紙にプロットしてみましょう。
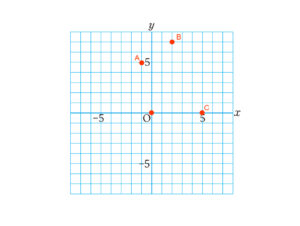
中学生なら直線ABの方程式をもとめ、その直線とy軸との交点を調べようとするでしょうか。
直線ABの方程式は・・
3(y-5)=2(x+1)
ですから、直線ABとy軸との交点は、これを点Kとして、
K(0,17/3)
すると三角形OAKの面積は・・
17/3×1×1/2=17/6
点Bからx軸に垂線を下ろし、その足をLとすると、
L(2,0)であり、台形OKBLの面積は・・
(17/3+7)×2×1/2=38/3
そして三角形BLCの面積は・・
7×3×1/2=21/2
四角形OABCの面積は・・
17/6+38/3+21/2=156/6=26
となります。
三角形OADの底辺の長さをxとして考えてよさそうなので・・
5x×1/2=26
すなわち、x=52/5
となります。
なりますが・・
xは点Dのx座標で、これは‐52/5であってもOKですよね。
うっかり52/5だけを答えにしてしまわないように気をつけてください。
※そんなわけですので、「三角形OADの底辺の長さをxとして考えてよさそうなので」とあいまいな表現を使っておきました。
そのほか、x>0を仮定しておいて、直線ACと直線BDが平行になるはずだ、と考えるアプローチもできますね。そうして求められるxの値は当然52/5だけになりますが、x軸の反対方向に底辺が伸びても同面積の三角形が描ける、と考えを加えれば‐52/5の方も見つけることができます。
また、最初のアプローチのように先に四角形OABCの面積を求める場合、高校生なら
三角形OABの面積
面積 = 1/2 × |(0×5 – (-1)×0) + (-1×7 – 2×5) + (2×0 – 0×7)|
= 1/2 × |-7 – 10|
= 1/2 × |-17|
= 17/2
三角形OBCの面積
面積 = 1/2 × |(0×7 – 2×0) + (2×0 – 5×7) + (5×0 – 0×0)|
= 1/2 × |-35|
= 35/2
として、これらをあわせて26と求められるようにはなっていて欲しいかな、と思います。

